En este artículo se tocará el tema de mecánica de roca aplicado al fracturamiento hidráulico. No se entrará en detalles ni en desarrollos matemáticos, se verá lo necesario para poder entender el diseño de una fractura.
La mecánica de roca (también llamada reología de rocas), es la ciencia teórica y aplicada del comportamiento mecánico de las rocas.
Parte de la teoría es aceptada por todos los especialistas, pero otros fenómenos que actúan dentro de la formación son interpretados de maneras diferentes según los “gurúes”, y por ende en la simulación de fracturamiento hidráulico.
Definición de Esfuerzo
Esfuerzo
El esfuerzo es una fuerza ejercida sobre un área, o sobre la superficie de un material. La fuerza puede ser perpendicular o tangencial al área.
Si el esfuerzo es perpendicular, o normal, a la superficie será un esfuerzo de compresión y es representado por σ.
Si en cambio el esfuerzo es tangencial a la superficie, o paralelo al plano, será un esfuerzo de corte, tendiendo a cortar el material en este plano. Es representado por τ.
Los esfuerzos son considerados positivos cuando son compresivos y negativos cuando son tensionales. En la Figura 1, se puede observar los tipos esfuerzos mencionados anteriormente.

Deformación Específica
Cuando aplicamos un esfuerzo a un cuerpo, inmediatamente ese cuerpo empieza a deformarse en una mayor o menor medida según el material.
Esa deformación específica (ε), que en inglés se llama “strain”, es la relación: cambio en la longitud sobre longitud original (ε=ΔL/L).
Por definición el término “strain” es adimensional. Para un esfuerzo de presión, la deformación del cuerpo corresponde a un acortamiento longitudinal y a una expansión transversal.
Por norma se considera el acortamiento como “strain” positivo y la expansión como “strain” negativo. En la Figura 2, se puede observar el efecto de deformación “strain”.

Esfuerzo in situ
En la formación, bajo tierra, cada cubo de roca esta sometido a una serie de esfuerzos. Podemos representar los esfuerzos según 3 ejes, los que van ser un esfuerzo vertical (σv) y dos esfuerzos horizontales de amplitudes diferentes, uno el máximo (σmax) y el otro mínimo (σmin).
El esfuerzo vertical representa el peso de las diferentes capas superiores a la capa estudiada. Su valor es normalmente en un rango de 0,98 a 1,1 psi/pie (en ausencia de datos tomar 1,0 psi/pie).
Este mismo esfuerzo tienen tendencia a deformar horizontalmente la roca generando esfuerzos horizontales. Pero ¿por qué los esfuerzos horizontales son diferentes según la dirección? Porque la roca esta sometida no solamente a la resultante del esfuerzo vertical pero también a esfuerzos resultantes de movimientos tectónicos del pasado.
Cuando se propaga una fractura, es porque las dos caras de la fractura se separan venciendo el esfuerzo in situ perpendicular a las caras.
La naturaleza de la mecánica de roca siempre busca el menor esfuerzo y en consecuencia la fractura va crecer perpendicularmente al esfuerzo mínimo.
Por lo tanto siempre existe una dirección preferencial de fractura que en la literatura se encuentra bajo el término de PFP (Preferred Fracture Plan), o plano preferencial de fractura.
Normalmente los esfuerzos horizontales son menores que el esfuerzo vertical, y por ende las fracturas crecen generalmente en un plano casi vertical (hay excepciones).
En caso de pozos poco profundos, menos de 300 m., el esfuerzo vertical puede ser el menor de los tres y en este caso la fractura puede ser horizontal.
A una profundidad intermedia es posible que se generen fracturas inclinadas porque el esfuerzo mínimo no es necesariamente vertical u horizontal.
Pero en la mayoría de los yacimientos productivos estamos lo suficientemente profundo y las fracturas son orientadas verticalmente.
También la cercanía a una falla puede influir sobre la orientación de las fracturas por su efecto sobre el estado de los esfuerzos.
La intensidad de los esfuerzos tiene otro efecto, que es el control de crecimiento en altura de la fractura. Los esfuerzos in situ son dependientes del tipo de mecánica de roca, las arcillas tienen esfuerzos horizontales mayores que las arenas.
El crecimiento en altura de la fractura va a ser limitado por la presencia de capas con mayores valores de esfuerzos por arriba o por debajo a la capa a fracturar.
El ancho de la fractura va a ser también dependiente de los esfuerzos y a mayor esfuerzo hay un menor ancho de fractura.
La presión de tratamiento que es la presión que necesitamos para empujar la roca en ambas caras de la fractura va a ser siempre superior al esfuerzo mínimo, y a mayor esfuerzo mínimo, mayor será la presión de fractura.
Esto es muy importante para nosotros porque puede implicar limitaciones para el equipamiento a utilizar en superficie. En la Figura 3, se puede observar un esquemático de los esfuerzos presentes en la mecánica de roca.

Esfuerzo Efectivo
Nos interesa conocer el esfuerzo real que los granos de arena de formación o los granos de agentes de sostén van a soportar. El fluido presente en los poros soporta parte del esfuerzo total, y los granos son sometidos solamente a una parte del esfuerzo ejercido por la roca. Este esfuerzo resultante es lo que llamamos esfuerzo efectivo.
La presión del fluido es la presión poral. El proceso de difusión, deformación y la cementación entre los granos afectan la eficiencia de la presión del fluido para soportar la carga aplicada a la formación.
Entonces solamente parte de esta presión poral es realmente efectiva y esa reducción de presión es representada por un coeficiente α, llamado coeficiente de poroelasticidad.
Entonces el esfuerzo efectivo sobre los granos (σ’) va a ser el esfuerzo in situ (σ) menos parte de la presión poral. σ’ = σ – αP. El coeficiente de poroelasticidad puede considerarse igual a 0,7 en condiciones normales in situ, y 1,0 dentro del empaque de agente de sostén.
De esta relación vemos que si hay cambios en la presión poral, esto implicará cambios en los esfuerzos sobre el agente de sostén. En la Figura 4, se observa un esquemático del esfuerzo efectivo en la formación.

Esfuerzos según la Formación
El esfuerzo vertical, σv, depende del peso de las capas de rocas superiores, independientemente del tipo de formación.
Pero los esfuerzos horizontales son distintos según el tipo de formación. Esta diferencia de esfuerzos depende de sí la formación es más o menos plástica.
Si la formación es muy plástica tiene tendencia a deformarse más y podemos imaginar como cada cubo de roca tendrá tendencia a empujar más los cubos de roca vecinos generando así más esfuerzos horizontales. O sea, más deformable es la formación, mayores serán los esfuerzos tangenciales horizontales.
Por esta razón, normalmente una arcilla es más plástica que una arena, la intensidad de los esfuerzos es mayor que en la arena.
La plasticidad esta representada por la Relación de Poisson (υ), que se encuentra definida como la relación de deformación lateral.
En consecuencia, esa relación es una medición de cuanto una roca se deformará horizontalmente cuando es sometida a una deformación vertical.
Las formaciones con mayores Relación de Poisson, como las arcillas, tenderán más a deformarse en el plano horizontal que formaciones con relaciones menores, como las areniscas (clásticas).
Como bajo tierra las capas no están libres de moverse, se generan esfuerzos horizontales dentro de las rocas. En la Figura 5, se muestran los esfuerzos según el tipo de formación.

Una manera rápida de estimar los gradientes de cierre de fractura es utilizando la siguiente fórmula:

(Ec. 1)
Donde:
- A = 0,4 para arenisca limpia (gamma ray = 40).
- A = 0,5 para arcilla (gamma ray = 100).
- σv = 1 psi/pie.
- B = 0,5.
- Pe = 0,43 psi/pie en un reservorio normalmente presurizado.
- C = efecto tectónico, generalmente 0, máximo 0,1 psi/pie.
Concentración de esfuerzos en la vecindad del pozo
En las secciones anteriores se ha hablado de los esfuerzos en la formación a una cierta distancia del pozo en una zona no disturbada.
Pero cuando se construye el pozo y se lo perfora, se modifican los esfuerzos en la vecindad de las paredes del pozo, o sea se modifica las condiciones de equilibrio en esta zona.
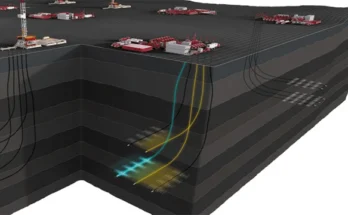
Desde el pozo hasta una distancia de uno o dos veces el diámetro del pozo se genera nuevas condiciones de equilibrio. Estas condiciones, en la zona de mayores esfuerzos que es la pared del pozo, son representadas por la ecuación de la Figura 6.
Vemos entonces que en esta zona hay una concentración de esfuerzos que pueden afectar el inicio de la fractura. La zona de concentración es menos de dos veces el diámetro del pozo, o sea por un pozo perforado con 9” tendremos condiciones normales a una distancia inferior a los 18”.
Módulo de Young
Definición
El Módulo de Young (E) representa la relación entre el esfuerzo que se aplica perpendicularmente al material y la deformación axial de ese material.
Se aplica una fuerza F y se obtiene un cambio de longitud ΔL. Graficando esta relación se obtiene el Módulo de Young. En un material homogéneo y elástico, como puede ser un metal, esta deformación es lineal en función al esfuerzo que se le aplica.
Desgraciadamente las rocas son un material no homogéneo y no elástico en todo rango de carga. Un material ideal tiene una relación esfuerzo/deformación lineal, pero las rocas no son un material ideal. Se toma la pendiente de la curva en la parte lineal para determinar el Módulo de Young.
Un alto valor de E representa un material muy duro, lo que significa que un alto esfuerzo (alta presión) es necesaria para deformar la roca. En la Figura 7, se observa una explicación gráfica del concepto del Módulo de Young.

Efecto de confinamiento
En la mecánica de roca, la roca no es un material ideal ya que tiene poros, micro-fisuras y otras heterogeneidades. Si a una muestra de roca le aplicamos presión sobre la circunferencia para simular el efecto de los esfuerzos in situ (presión de confinamiento), y aplicamos una fuerza en las extremidades, se observa que la deformación cambia según la presión de confinamiento.
Para cada presión de confinamiento obtenemos un gráfico diferente. En la formación, la roca siempre está comprimida, o confinada, por los esfuerzos naturales in situ. Entonces, en el laboratorio debemos tratar de simular siempre las condiciones de fondo.
Por lo tanto se necesita conocer los valores del esfuerzo mínimo, o de confinamiento, y realizar los respectivos ensayos con estos valores.
De otra manera los valores de Módulo de Young que se obtendrían no serían válidos. En la Figura 8, se puede observar el efecto de confinamiento en la determinación del Módulo de Young.

Arenisca típica
Si en un ensayo de laboratorio se toma una muestra de arenisca sometida a una presión de confinamiento equivalente a los esfuerzos in situ, se puede observar tres fases diferentes en la curva de deformación versus el esfuerzo.
En la primera fase la pendiente es grande, lo que representaría un Módulo de Young muy bajo, porque se están cerrando los poros y microfracturas que hay en la muestra.
La segunda fase es un período mucho más largo donde la muestra se deforma de manera lineal. En este período de deformación es casi elástica y es el período que consideramos para determinar el valor de E.
En la tercera fase la muestra empieza a deformarse cada vez más, rompiéndose posteriormente. En esta fase se ha sobrepasado el período de elasticidad en la mecánica de roca. Considerando las deformaciones longitudinal y lateral se calcula la deformación volumétrica.
En la Figura 9, se observa que en la fase 3 el volumen incremento a pesar del incremento de la carga. Es importante recordar este fenómeno, llamado dilatancia, que se encuentra explicado en el artículo de Mecánica de Roca aplicada al Fracturamiento Hidráulico.

Efecto de la mecánica de roca sobre la geometría de fractura
¿Cuál es la importancia del Módulo de Young sobre la geometría de una fractura?
El módulo de Young es la relación entre es esfuerzo perpendicular al material y la deformación de este material. Entonces por un mismo esfuerzo, a mayor Módulo de Young (formación más dura) menor deformación, es decir, menor movimiento de la cara de la fractura, lo que implica menor ancho de fractura.
Al inverso a menor Módulo de Young (formación blanda), mayor deformación, es decir, mayor ancho de fractura. En formaciones duras, se necesitaría mayor presión neta para obtener el ancho deseado, pero mayor presión neta significa crecimiento vertical de la fractura.
Cuando la altura de la fractura cubre varias capas con módulos de Young diferentes, el ancho no será uniforme en altura.
En consecuencia podría haber zonas (pinch point) donde el ancho no es suficiente para el paso del agente de sostén, provocando un arenamiento en esta zona. En la Figura 10, se puede observar el efecto del Módulo de Young versus el ancho de fractura en formación de distinta litología.

Factores que afectan la determinación de E en laboratorio
Si se necesita la determinación del Módulo de Young (E) en el laboratorio, el ensayo es bastante delicado de realizar. No hay muchos laboratorios equipados para hacerlo.
Se necesita contar con una celda tri-axial para poder confinar la muestra. La muestra debe ser elegida con cuidado, no debe tener anisotropía, ni fisuras, es decir, debe ser homogénea.
El contenido de humedad de la muestra debe representar las condiciones de fondo, presión y saturación. Si no se realizan correctamente estos ensayos, no son representativos de nada.
Además de que los ensayos son costosos, las operadoras evitan este tipo de estudio, y buscan definir valores de Módulo de Young utilizando otras técnicas como el perfilaje (logging).
Relación de Poisson
La Relación de Poisson representa la deformación lateral (perpendicular a la dirección del esfuerzo) de un material sometido a un esfuerzo longitudinal.
Para un diseño de fractura el valor de la Relación de Poisson no tiene mucha importancia, a menos de utilizarlo para calcular los esfuerzos in situ teóricos.
La deformación de las caras de la fractura es perpendicular al esfuerzo de la presión neta y es más representada por el Módulo de Young. Rocas con altas relaciones de Poisson transfieren mayor cantidad del esfuerzo vertical en la dirección horizontal, o sea resultan en mayores valores de esfuerzos horizontales.
Las arcillas que tienen mayor relación de Poisson que las arenas, tienen generalmente mayores valores de esfuerzo. Debido al comportamiento no lineal de las rocas, la relación de Poisson no es constante en todo el rango de esfuerzo.
Es afectado por los mismos factores que el Módulo de Young. En la Figura 11, se observa una representación de la determinación de la Relación de Poisson.

Determinación de las propiedades de mecánica de roca vía perfiles
Características de la roca deducidas de los perfiles
Se ha visto que es difícil conseguir valores de Módulo de Young, y de Relación de Poisson, desde muestras de núcleos. Entonces debemos deducirlos de perfiles sónico dipolar.
Esos perfiles miden el tiempo de propagación de la onda de corte y de la onda compresiva. Hay una relación matemática entre estos dos tiempos de propagación con la cual podemos calcular la Relación de Poisson.
Con la Relación de Poisson y la densidad de la formación podemos calcular el Módulo de Young. No se debe tomar la interpretación de los perfiles de forma automática. Los valores que obtenemos así son valores dinámicos del Módulo de Young.
La señal sonora es muy rápida y se mide un movimiento muy rápido dentro de la formación. En el laboratorio se aplica el esfuerzo muy lentamente sobre la muestra, lo que puede ser considerado estática.
Durante el proceso de fractura cuando se rompe la roca, el movimiento es probablemente más rápido que lo que se hace en el laboratorio, pero es mucho más lento que la velocidad del sonido, entonces lo podemos considerar como algo estático.
Para simular la fractura, se utilizan valores estáticos de Módulo de Young. Para deducirlos se han desarrollado correlaciones entre valores dinámicos y valores estáticos.

(Ec. 2)

(Ec. 3)

(Ec. 4)
Donde:
- ΔTs = Tiempo de propagación de la onda de corte.
- ΔTc = Tiempo de propagación de la onda de compresión.
- ρb = “módulo de volumen”.
- Edyn = Módulo de Young dinámico.
- v = Coeficiente de Poisson.
- G = Módulo de corte.
Módulo de Young dinámico vs. estático
No hay una fórmula matemática directa, ni relación directa entre en Módulo de Young dinámico y estático. Lo único que existe son relaciones empíricas determinadas en laboratorio, tomando varias muestras con las cuales se llevó a cabo el ensayo de laboratorio y al mismo tiempo se realizó un ensayo sónico. Se han publicado varias correlaciones.
La que se muestra en este gráfico es la correlación determinada por Morales (SPE 26561). Él relacionó el Módulo de Young estático.
Esta correlación se puede utilizar como guía, pero debería ser calibrada en cada zona con muestras de núcleo. En caso de no tener tampoco datos de perfil sónico dipolar, se puede estimar el Módulo de Young estático utilizando la siguiente ecuación:

(Ec. 5)
Donde:
- Øe = Porosidad efectiva.
Si te ha gustado este artículo y sientes que aporta valor, te invitamos a compartirlo en tus redes sociales preferidas, así nos ayudas a difundir información a todo a quien pueda interesar. Si tienes alguna duda, comentario o sugerencia, puedes dejarlo abajo en la sección de comentarios. ¡Nos interesa tu opinión!