El Factor de Forma de Dietz (CA) es un concepto fundamental y de larga data en la ingeniería de yacimientos, cuyo desarrollo se remonta a mediados del siglo XX.
Su origen está intrínsecamente ligado a la creciente necesidad de refinar las ecuaciones de productividad de pozos para yacimientos con geometrías de drenaje que se desviaban de las idealizaciones cilíndricas simplificadas.
Antes de su concepción, los modelos de flujo en medios porosos a menudo asumían geometrías ideales, lo que limitaba la precisión en la predicción del rendimiento real de los pozos.
La base para el desarrollo de los factores de forma fue establecida por Matthews et al. (1954), quienes realizaron estudios pioneros sobre el comportamiento de la presión en yacimientos no simétricos pero homogéneos.
Su trabajo condujo al desarrollo de una función dependiente de la forma, la cual representó un avance significativo al reconocer que la geometría del área de drenaje influía directamente en el comportamiento de la presión.
Esta función fue posteriormente adoptada y expandida por Brons & Miller (1961) y, de manera más notable, por Dietz (1965).
Dietz consolidó estos avances al presentar soluciones analíticas para una variedad de geometrías de yacimientos regulares y al compilar una tabla de factores de forma específicos para diferentes configuraciones (como círculos, cuadrados y triángulos) y diversas ubicaciones de pozos dentro de estas geometrías.
El CA es ampliamente reconocido como uno de los parámetros clave en la ecuación de productividad, siendo indispensable para predecir con precisión el rendimiento de producción de pozos de petróleo y gas.
Su introducción fue crucial para corregir las desviaciones de las suposiciones simplificadas inherentes a las ecuaciones de productividad más básicas, tales como la penetración parcial del pozo o su ubicación no centrada dentro del área de drenaje.
La aparición del factor de forma de Dietz, por lo tanto, representa un hito en la ingeniería de yacimientos. Este avance marcó una transición fundamental de modelos excesivamente simplificados a herramientas analíticas más realistas, capaces de cuantificar el impacto de la geometría del área de drenaje y la ubicación del pozo en el rendimiento de producción.
Su desarrollo fue una respuesta directa a la necesidad de mejorar la precisión en la predicción del comportamiento de los pozos en escenarios de yacimientos acotados, proporcionando una herramienta esencial para el análisis y la gestión de la producción.
Definición Fundamental y Propósito en las Ecuaciones de Productividad
El factor de forma de Dietz, denotado como CA, es un parámetro adimensional cuyo propósito principal es generalizar la forma del área de drenaje de un pozo en condiciones de régimen de flujo estabilizado o pseudo-estado estacionario (PSS).
En esencia, este factor permite que las ecuaciones de productividad, originalmente derivadas para geometrías ideales como un pozo centrado en un yacimiento circular, sean aplicables a una gama mucho más amplia de configuraciones de yacimientos con límites definidos.
Sin el CA, las soluciones analíticas estarían severamente restringidas a condiciones ideales, lo que limitaría su utilidad práctica en la mayoría de los yacimientos reales.
Por ejemplo, para un pozo centrado en un yacimiento circular, el valor de CA es 31.62. Este valor específico sirve como un punto de referencia que valida la aplicabilidad del factor de forma a geometrías más complejas.
El factor de Dietz se integra de manera fundamental en la ecuación de pseudo-estado estacionario para corregir la suposición de drenaje radial con pozo centrado.
Esta integración permite que los ingenieros utilicen formulaciones analíticas para estimar el rendimiento de pozos en una variedad de formas de yacimiento y ubicaciones de pozo. De otro modo requeriría simulaciones numéricas considerablemente más complejas y costosas.
De esta manera, el CA actúa como un puente matemático, conectando los modelos analíticos simplificados de flujo en yacimientos con la inherente complejidad de las geometrías de drenaje reales.
Desarrollo Teórico y Derivación del Factor de Dietz
Ecuación de Flujo Pseudo-Estado Estacionario y la incorporación de CA
El factor de forma de Dietz es un componente intrínseco de la ecuación de régimen de flujo en pseudo-estado estacionario (PSS).
Es una condición de flujo que se establece en un yacimiento acotado después de que el transitorio de presión inicial ha alcanzado los límites exteriores del yacimiento.
En este régimen, la tasa de cambio de presión es constante en todos los puntos del yacimiento, lo que permite un análisis simplificado del comportamiento del flujo.
La ecuación general de régimen de flujo en pseudo-estado estacionario para líquidos ligeramente compresibles en un sistema de flujo radial incorpora el factor de forma de Dietz (CA). Una forma común de esta ecuación para la caída de presión (ΔP) en un pozo es:
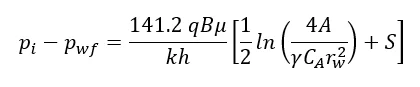
(Ec. 1)
Donde:
- pi = Presión inicial del yacimiento
- pwf = Presión de fondo fluyente
- q = Tasa de producción
- B = Factor volumétrico del fluido
- h = Espesor del yacimiento
- rw = Radio del pozo
- S = Factor de daño
- γ = Exponencial de la constante de Euler (1.781)
En esta formulación, el término ln(4A/(γCArw2)) es fundamental. Este término reemplaza al más simple ln(re/rw) que se encuentra en la ecuación de flujo radial en estado estacionario para un yacimiento circular con un pozo centrado.
Al incorporar el CA, la ecuación se generaliza para describir la relación presión-caudal en cualquier forma de área de drenaje cerrada, no solo la circular1.
La incorporación de CA en la ecuación del régimen de flujo en pseudo-estado estacionario no es simplemente un ajuste empírico, sino una generalización matemática que permite que la misma formulación analítica describa el comportamiento de presión de pozos en diversas geometrías de drenaje cerradas.
Esta característica subraya la versatilidad y la elegancia del concepto de Dietz, ya que simplifica problemas de flujo que, de otro modo, requerirían soluciones mucho más complejas o numéricas2.
Suposiciones en la Derivación del Factor de Forma
La derivación clásica del factor de forma de Dietz para las ecuaciones de productividad se basa en un conjunto de suposiciones altamente idealizadas sobre el yacimiento y los fluidos.
Estas suposiciones son necesarias para permitir la obtención de soluciones analíticas y definen estrictamente el dominio de aplicabilidad del CA:
- Medio Poroso Homogéneo: Se asume que las propiedades petrofísicas del yacimiento, como la porosidad y la permeabilidad, son uniformes y constantes en toda el área de drenaje.
- Espesor de Capa Neta Uniforme: El espesor de la formación productora se considera constante a lo largo del yacimiento.
- Fluido de Compresibilidad Pequeña y Constante: La formulación es válida para líquidos con una compresibilidad baja y constante, lo que a menudo se aplica a petróleo subsaturado o agua.
- Pequeños Gradientes de Presión: Los cambios de presión a través del yacimiento se consideran despreciables, lo que permite simplificaciones en las ecuaciones de flujo.
- Fuerzas Gravitacionales Despreciables: Los efectos de la gravedad sobre el flujo de fluidos dentro del área de drenaje se ignoran, lo que es razonable en formaciones horizontales y delgadas.
- Flujo Monofásico: La formulación original del CA está diseñada para el flujo de una sola fase de fluido, típicamente líquido. Esto limita su aplicabilidad directa en escenarios de flujo multifásico.
- Pozo Completamente Penetrante y Vertical: Las soluciones de Dietz (1965) se derivaron principalmente para pozos verticales que penetran completamente el espesor de la formación.
La dependencia del CA de la homogeneidad, isotropía y flujo monofásico es la causa fundamental de sus limitaciones en yacimientos geológicamente complejos o con fluidos multifásicos.
Estas condiciones idealizadas, si bien facilitaron su derivación analítica y su amplia adopción inicial, definen estrictamente su dominio de aplicabilidad y explican por qué se requieren métodos más avanzados para escenarios de yacimientos más realistas. Estas limitaciones serán abordadas más adelante.
Metodología del Método de Imágenes para el Cálculo de CA en Geometrías Regulares
El método principal para calcular los factores de forma de Dietz para geometrías de drenaje regulares es el «método de imágenes».
Esta técnica, que tiene una analogía directa con su uso en electrostática para resolver problemas de campo potencial, permite abordar la ecuación de la difusividad para un pozo de producción en un yacimiento con límites cerrados y no-flujo.
La metodología implica la introducción de pozos «imagen» fuera de los límites del yacimiento real.
Estos pozos imagen se colocan de manera estratégica, como espejos, para satisfacer las condiciones de contorno de no-flujo (límites impermeables) en las fronteras del yacimiento.
La superposición de las soluciones de presión generadas por los pozos reales y sus imágenes crea un patrón de flujo que replica con precisión el comportamiento de un pozo en un yacimiento acotado.
Cada pozo imagen contribuye a la distribución de presión de tal manera que la presión neta en las fronteras del yacimiento se mantiene constante o el flujo a través de ellas es cero, simulando un límite físico.
Este método es particularmente efectivo y ha sido ampliamente utilizado para geometrías regulares y simétricas, como rectángulos o cuadrados, así como para diversas ubicaciones de pozos dentro de estas geometrías.
La complejidad del cálculo del CA mediante el método de imágenes aumenta exponencialmente con el número de límites y la irregularidad de la geometría, ya que cada límite adicional requiere la inclusión de más pozos imagen para mantener las condiciones de contorno3.
A pesar de su eficacia para geometrías ideales, el método de imágenes se vuelve computacionalmente intensivo o incluso inviable para formas irregulares o yacimientos con configuraciones de límites complejas.
Esta limitación inherente subraya una compensación fundamental en la ingeniería de yacimientos: la simplicidad y elegancia de las soluciones analíticas a menudo conllevan un costo en la representatividad de la complejidad geológica.
Sin embargo, investigaciones más recientes han buscado refinar la aplicación del CA incluso dentro de su marco analítico.
Por ejemplo, se han desarrollado correlaciones basadas en funciones gaussianas para la estimación del factor de forma de Dietz en áreas de yacimientos rectangulares homogéneas con relaciones de aspecto entre 2 y 54.
Estas correlaciones han demostrado una buena concordancia con los valores calculados mediante el método de imágenes, especialmente para ubicaciones de pozos cercanas a los límites del yacimiento.
Esto indica un esfuerzo continuo por optimizar y simplificar la aplicación del CA en escenarios donde aún es pertinente.
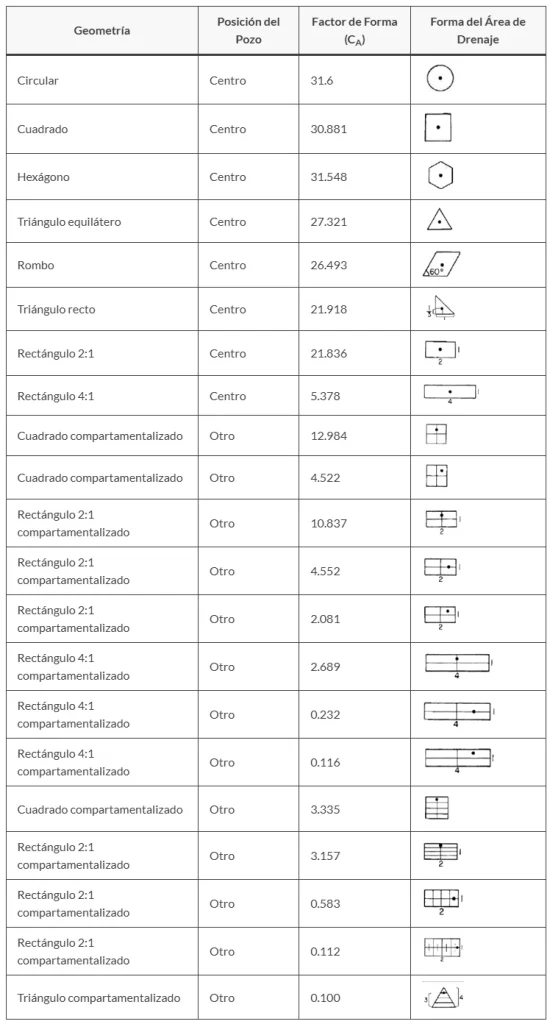
Valores del Factor de Forma
El factor de forma CA varía significativamente según la geometría del yacimiento y la posición del pozo. Algunos valores típicos incluyen:
Aplicaciones del Factor de Forma de Dietz en la Ingeniería de Reservorio
Análisis de Prueba de Pozos y Caracterización del Área de Drenaje
Una de las aplicaciones más importantes del factor de forma de Dietz es en el análisis de pruebas de pozos, particularmente en el régimen de pseudo-estado estacionario.
En este contexto, el CA permite estimar el tamaño y la forma del área de drenaje de un pozo a partir de datos de producción, como las presiones de fondo de pozo y los caudales.
Esta capacidad de cuantificación es vital para comprender cómo un pozo individual está interactuando con los límites del yacimiento, lo que a su vez permite inferir sobre la densidad de pozos y la gestión general del yacimiento.
La aplicación de CA en este contexto transforma el análisis de pruebas de pozos de una interpretación meramente cualitativa a una cuantificación precisa de la geometría del área de drenaje.
Esta precisión es vital para la ingeniería de yacimientos, ya que proporciona una comprensión detallada de cómo un pozo individual está influenciando y siendo influenciado por su entorno de yacimiento.
Estimación de Productividad de Pozos y Optimización de Patrones de Drenaje
El factor de forma de Dietz es un componente esencial en las ecuaciones de productividad, ya que permite cuantificar el impacto de la ubicación del pozo y la penetración parcial en el rendimiento de producción.
Esta capacidad es de gran importancia en la fase de desarrollo de campos, donde el diseño de patrones de pozos, la determinación del espaciamiento óptimo entre ellos y la estimación de la productividad individual de cada pozo son decisiones críticas.
Una comprensión precisa de las formas de drenaje de los pozos, facilitada por el CA, es fundamental para optimizar la ubicación de los pozos y maximizar las reservas recuperables del yacimiento.
Al predecir cómo diferentes configuraciones geométricas afectan el flujo hacia el pozo, los ingenieros pueden tomar decisiones para mejorar la eficiencia de la producción.
Permite a los ingenieros diseñar proactivamente la ubicación y el espaciamiento de los pozos para optimizar la recuperación de hidrocarburos y mejorar finalmente la rentabilidad.
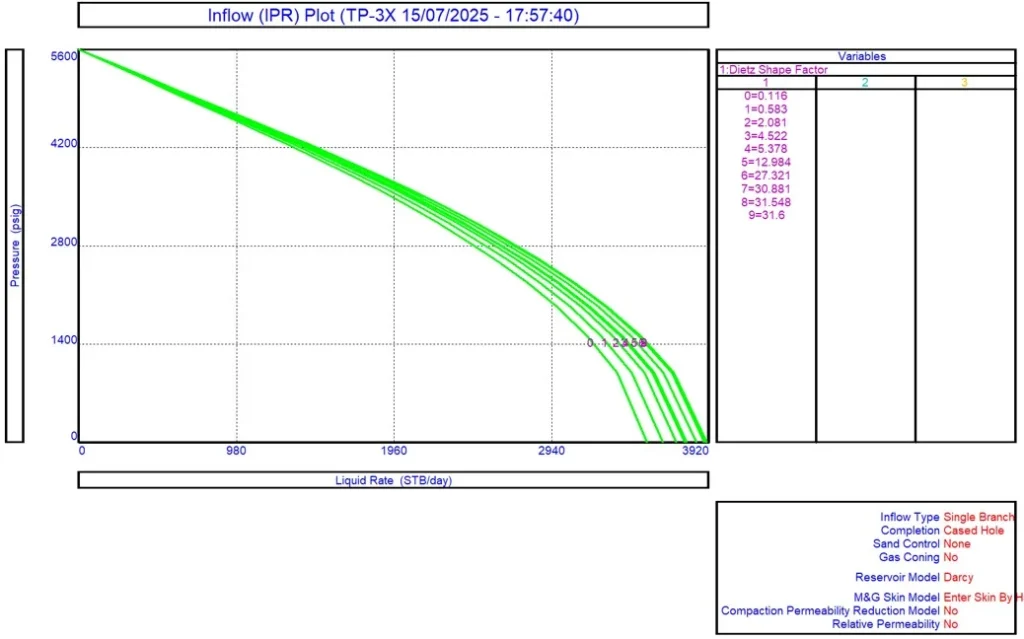
Para fines simplementes teóricos, en la Figura 1, se puede observar una sensibilidad de Factor de Forma de Dietz suponiendo diferentes geometrías de yacimiento y su impacto en la la tasa de producción.
Se usó el software Prosper, utilizando valores de geometría circular de 31.6 (caso más favorable), hasta una geometría de rectágulo 4:1 compartamentalizado, con una ubicación del pozo distinta al centro (caso menos favorable).
Principales Limitaciones del Factor de Forma de Dietz
El Factor de Forma de Dietz (CA), aunque es un concepto fundamental para el análisis de la productividad de pozos en yacimientos acotados bajo condiciones de régimen de flujo pseudo-estado estacionario, presenta limitaciones significativas en la ingeniería de yacimientos moderna.
Principalmente, su derivación se basa en suposiciones altamente idealizadas: un medio poroso homogéneo e isotrópico con espesor uniforme.
Esto contrasta marcadamente con la realidad de los yacimientos, que en su gran mayoría son heterogéneos (variaciones espaciales en propiedades) y anisotrópicos (permeabilidad dependiente de la dirección), lo que reduce la precisión de la aplicación directa del CA.
Además, las soluciones originales del CA se desarrollaron para pozos verticales en geometrías regulares y simétricas. Esto limita su utilidad para los tipos de pozos no convencionales actuales, como los pozos horizontales o multifracturados.
Estos pozos complejos exhiben regímenes de flujo lineal o dominados por fracturas que pueden persistir durante años, a menudo sin alcanzar el pseudo-estado estacionario requerido para la aplicabilidad del CA.
El factor de forma asume un flujo monofásico de un líquido con compresibilidad y viscosidad pequeñas y constantes.
Esto lo hace menos adecuado para escenarios de flujo multifásico (petróleo, gas, agua) o cuando se trata de fluidos no newtonianos (como el petróleo pesado), donde las propiedades del fluido cambian drásticamente con la presión y la temperatura.
Estas simplificaciones inherentes requieren el uso de modelos numéricos y analíticos más avanzados para una caracterización y predicción precisas en los complejos entornos de yacimientos actuales.
Referencias:
- Blasingame, T. (1997). Pseudosteady-State Flow Relations for a Radial System. Texas: Texas A&M U. Recuperado desde: https://blasingame.engr.tamu.edu/z_zCourse_Archive/P620_16C/P620_16C_Lectures_(working_lectures)/20161020_P620_16C_Lec_16_(Work)_Mod3_FunFld_04_PSS_Flow_[PDF].pdf ↩︎
- Astafev, V., Roters, P., & Tjan, V. (2018). Analytical Evaluation of Well Productivity Index and Dietz Shape Factor for Double-periodic Multi-well Reservoir Systems. International Conference on Applied Mathematics & Computer Science (ICAMCS). doi:0.1109/ICAMCS46079.2018.000-4 ↩︎
- Tehrani, D., Chen, G., & Peden, J. (1998). Finding a regular geometry for an irregular reservoir shape for well performance calculations. Petroleum Geoscience, 4(4), 349-352. doi:https://doi.org/10.1144/petgeo.4.4.349 ↩︎
- Polat, C. (2021). Gaussian formulation based correlation for Dietz shape factor. Upstream Oil and Gas Technology. doi:10.1016/j.upstre.2021.100059 ↩︎
Si te ha gustado este artículo y crees que es valioso, compártelo en tus redes sociales para ayudarnos a difundir la información. Si tienes dudas, comentarios o sugerencias, déjalos en la sección de comentarios. ¡Valoramos tu opinión!